

For a function, its inverse admits an explicit description: it sends each element to the unique element such that f(x) y. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by. Graph functions, plot points, visualize algebraic equations, add sliders, animate graphs, and more. In mathematics, the inverse function of a function f (also called the inverse of f) is a function that undoes the operation of f.
#INVERSE GRAPH FREE#
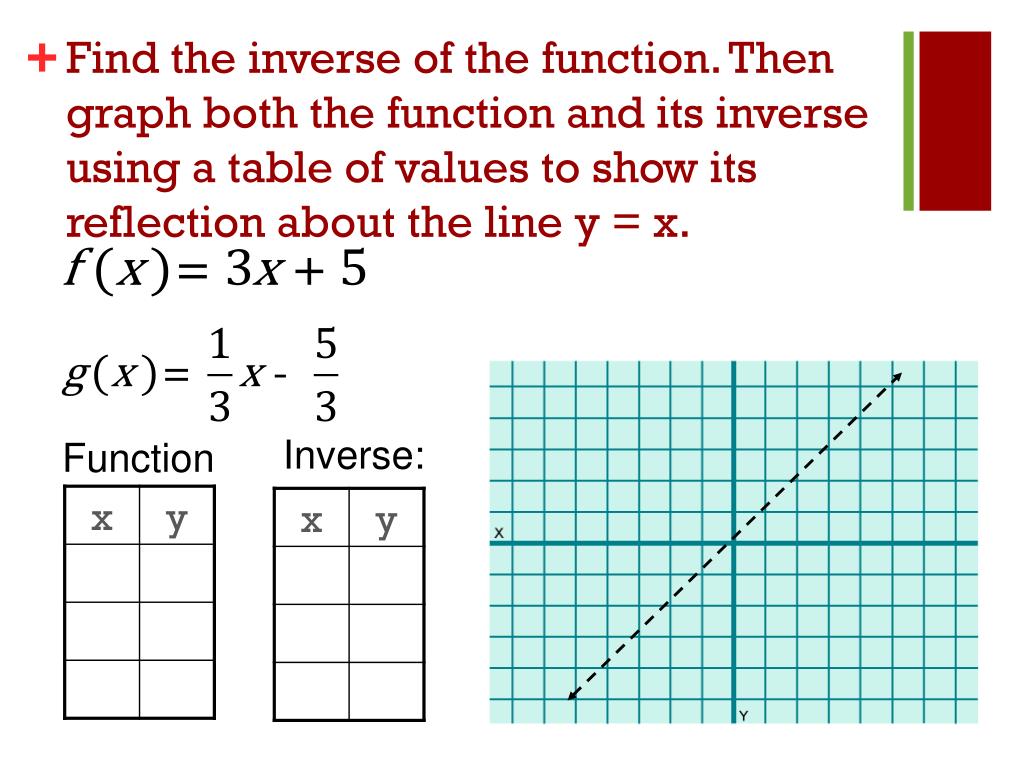
In order for a function to have an inverse, it must be a one-to-one function. The inverse graph of G denoted by (G) is a graph whose set of vertices coincides with G such that two distinct vertices x and y are adjacent if either xyS or yxS. Explore math with our beautiful, free online graphing calculator. If you want to think about this graphically, f(x) and its inverse function will be reflections across the line y x. If f(x) says to multiply by 2 and then add 1, then the inverse f(x) will say to subtract 1 and then divide by 2. But an output from a function is an input to its inverse if this inverse input corresponds to more than one inverse output (input of the original function), then the “inverse” is not a function at all! To put it differently, the quadratic function is not a one-to-one function it fails the horizontal line test, so it does not have an inverse function. An inverse function essentially undoes the effects of the original function. This means that any point in the function becomes.
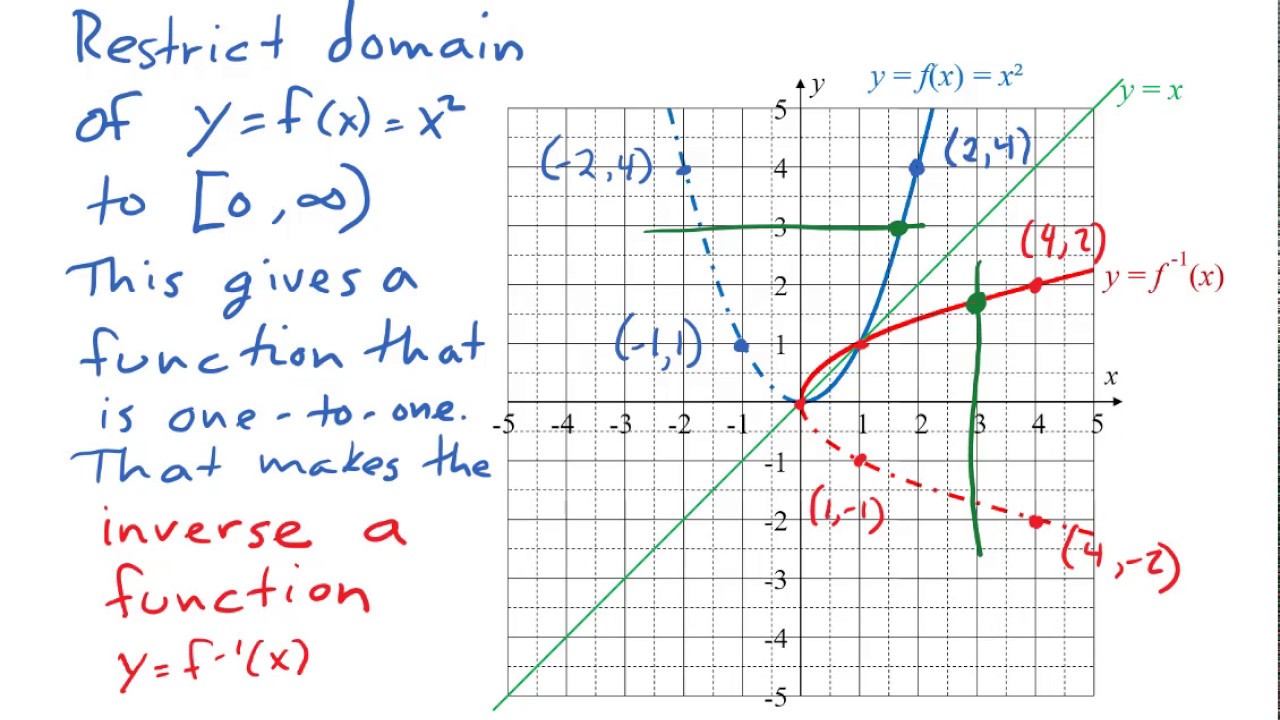
For example, the output 9 from the quadratic function corresponds to the inputs 3 and –3. Plotting the inverse of a function is the same method for any function. If we want to construct an inverse to this function, we run into a problem, because for every given output of the quadratic function, there are two corresponding inputs (except when the input is 0). We can look at this problem from the other side, starting with the square (toolkit quadratic) function \(f(x)=x^2\). Notice that no horizontal line intersects the graph more than once.


 0 kommentar(er)
0 kommentar(er)
